Кенингсбергские мосты и теория графов …

А знаете ли вы, что семь мостов города Кенингсберга (сейчас этот город называется Калининград) стали «виновниками» создания Леонардом Эйлером теории графов (Граф – это определенное количество узлов (вершин), соединённых рёбрами). Но как, же это произошло?

Два острова и берега на реке Прегель, на которой стоял Кенингсберг, были соединены 7 мостами. Знаменитый философ  и ученый Иммануил Кант, гуляя по мостам города Кенигсберга, поставил задачу, известную всем в мире как задача о 7 кенигсбергских мостах: можно ли пройти по всем данным мостам и при этом вернуться в исходную точку маршрута так, чтобы пройти по каждому мосту только 1 раз. Многие пытались решить данную задачу как практически, так и теоретически. Но никому это не удавалось, при этом и не удавалось доказать, что это невозможно даже теоретически. Поэтому, по историческим данным, считается, что в 17 веке у жителей сформировалось особая традиция: прогуливаясь по городу, пройти по всем мостам всего по 1 разу. Но, как известно, ни у кого это не получилось.

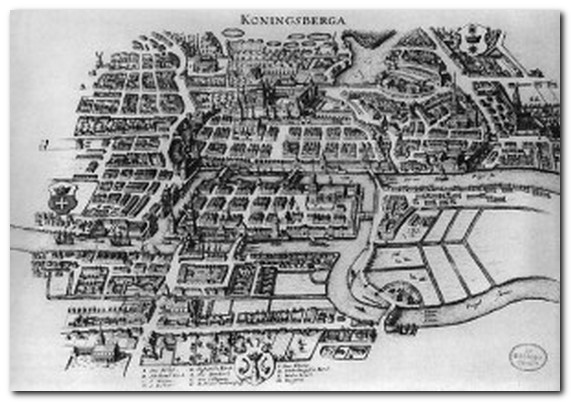
В 1736 г. данная задачка заинтересовала ученого Леонарда Эйлера, выдающегося и знаменитого математика и члена Петербургской академии наук. Об этом он написал в письме своему другу – ученному, итальянскому инженеру и математику Мариони от 13 марта 1736 г. Он нашел правило, используя которое можно было легко и просто получить ответ на данный интересующий всех вопрос. В случае с городом Кенингсберг и его мостами это оказалось невозможно. В процессе своих рассуждений, Эйлер пришел к следующим теоретическим выводам: - Число нечётных вершин (вершин, к которым ведёт нечётное число рёбер) графа должно быть чётно. Не может существовать граф, который имел бы нечётное число нечётных вершин. - Если все вершины графа чётные, то можно, не отрывая карандаша от бумаги, начертить граф, при этом можно начинать с любой вершины графа и завершить его в той же вершине. - Граф с более чем 2 нечётными вершинами невозможно начертить одним росчерком.

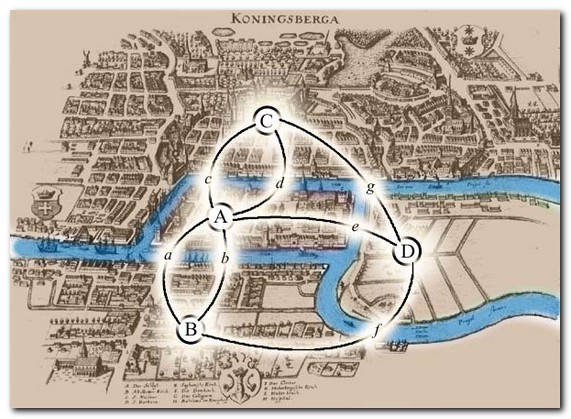
Если рассматривать данное правило к 7 мостам Кенингсберга, то части города на рисунке (графе) обозначаются вершинами, а мосты – ребрами, соединяющими данные вершины. Граф 7 кёнигсбергских мостов имел 4 нечётные вершины (то есть все, его вершины были нечетные), следовательно, невозможно пройти по всем 7 мостам, не проходя ни по одному из них дважды. Казалось бы, у такого необычного открытия не может быть никакого реального применения и практической пользы. Но применение нашлось, и еще какое. Теория графов, созданная Леонардом Эйлером, легла в основу проектирования коммуникационных и транспортных систем, она используется в программировании  и информатике, в физике, химии и многих других науках и областях.

justify

Но самое интересное в том, что историки считают, что есть человек, который решил данную задачу, он смог пройти через все мосты только один раз, правда теоретически, но решение было…. А произошло это вот как... Кайзер (император) Вильгельм славился своей простотой мышления, прямотой и солдатской «недалёкостью». Однажды, находясь на светском рауте, он чуть не стал жертвой шутки, которую с ним решили сыграть учёные умы, присутствующие на данном приёме. Они показали кайзеру карту города Кёнигсберга, и попросили его попробовать решить эту знаменитую задачку, которая по определению была просто не решаемой. К всеобщему удивлению, Кайзер попросил лист бумаги и перо, и при этом уточнил, что решит данную задачку всего за полторы минуты. Ошеломлённые ученные не могли поверить своим ушам, но чернила и бумагу быстро нашли для него. Кайзер положил листок на стол, взял перо, и написал: «Приказываю построить восьмой мост на острове Ломзе». И все задача решена….. Так в городе Кёнигсберг и появился новый 8 мост через реку, который так и назвали — мост Кайзера. А задачку с 8 мостами теперь может решить даже ребёнок.