Разработана теория квантовой машины Силарда

Физики из Токийского университета рассмотрели работу машины Силарда, которая иллюстрирует идею демона Максвелла, в квантовом случае.
 Демон, гипотетическое разумное существо, был придуман в 1867 году. Мысленный эксперимент Джеймса Максвелла очень прост: нужно представить себе герметичный сосуд, разделённый на две части, заполненные одним и тем же газом при одной и той же температуре. В непроницаемой перегородке сделана дверца, которую контролирует тот самый демон; молекулы, движущиеся с высокой скоростью, он пропускает только из левой части сосуда в правую, а «медленные» молекулы — в обратном направлении. Получается, демон нагревает правую часть и охлаждает левую без подвода энергии к системе, а это противоречит второму началу термодинамики.
Демон Максвелла, ставший одним из самых известных мысленных экспериментов, привлёк внимание многих учёных. Классический анализ мнимого парадокса провёл в 1929 году американский физик Лео Силард, указавший на то, что демону, очевидно, необходимо как-то измерять скорость молекул, и на получение этой информации ему придётся затратить энергию.
В машине Силарда используется одна классическая частица, помещённая в герметичную камеру с постоянной температурой T. Внешний наблюдатель устанавливает стенку в центре камеры и определяет, в каком из двух отсеков оказалась частица, а затем прикрепляет к стенке некий груз. При последующем изотермическом расширении можно получить k•T•ln2 единиц энергии (уменьшить энтропию на k•ln2), где k — постоянная Больцмана. Второе начало термодинамики говорит о том, что это уменьшение, если мы включаем в рассмотрение наблюдателя, должно компенсироваться ростом энтропии, и такой рост действительно происходит при получении одного бита информации о местонахождении частицы (или стирании результатов измерений).
Демон, гипотетическое разумное существо, был придуман в 1867 году. Мысленный эксперимент Джеймса Максвелла очень прост: нужно представить себе герметичный сосуд, разделённый на две части, заполненные одним и тем же газом при одной и той же температуре. В непроницаемой перегородке сделана дверца, которую контролирует тот самый демон; молекулы, движущиеся с высокой скоростью, он пропускает только из левой части сосуда в правую, а «медленные» молекулы — в обратном направлении. Получается, демон нагревает правую часть и охлаждает левую без подвода энергии к системе, а это противоречит второму началу термодинамики.
Демон Максвелла, ставший одним из самых известных мысленных экспериментов, привлёк внимание многих учёных. Классический анализ мнимого парадокса провёл в 1929 году американский физик Лео Силард, указавший на то, что демону, очевидно, необходимо как-то измерять скорость молекул, и на получение этой информации ему придётся затратить энергию.
В машине Силарда используется одна классическая частица, помещённая в герметичную камеру с постоянной температурой T. Внешний наблюдатель устанавливает стенку в центре камеры и определяет, в каком из двух отсеков оказалась частица, а затем прикрепляет к стенке некий груз. При последующем изотермическом расширении можно получить k•T•ln2 единиц энергии (уменьшить энтропию на k•ln2), где k — постоянная Больцмана. Второе начало термодинамики говорит о том, что это уменьшение, если мы включаем в рассмотрение наблюдателя, должно компенсироваться ростом энтропии, и такой рост действительно происходит при получении одного бита информации о местонахождении частицы (или стирании результатов измерений).
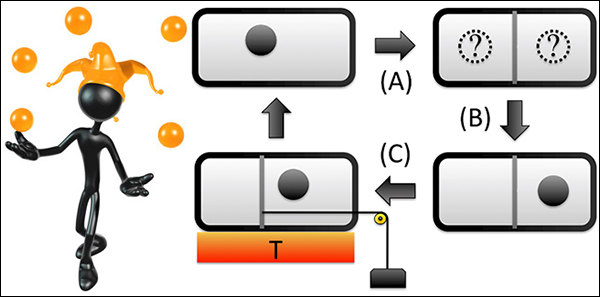


Демон Максвелла и схема действия классической машины Силарда (иллюстрации Shutterstock.com / Scott Maxwell / LuMaxArt, S. W. Kim et al.).
Заметим, что в классическом случае установку и удаление стенки считают действием, которое совершается без расходования энергии. В рассмотренной японскими учёными квантовой версии такое упрощение неприменимо; авторы учли этот факт и составили теоретическое описание машины Силарда для произвольного числа частиц.
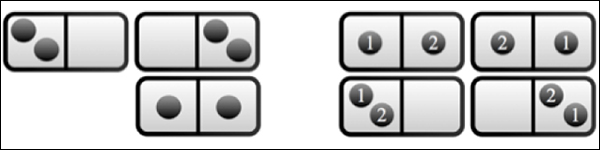
Простейший вариант двух частиц хорошо иллюстрирует результаты вычислений. Здесь, как рассчитали физики, в одном рабочем цикле машины Силарда можно извлечь 2•k•T•f0•lnf0 единиц энергии, где f0 — вероятность обнаружения обеих частиц в одной из частей камеры. В случае различимых частиц f0 = 0,25, и тогда выражение преобразуется в классическую формулу, указанную выше. Кажется, что результат должен быть больше, поскольку при измерении мы получаем два бита информации, но уменьшение объясняется довольно просто: дело в том, что два из четырёх возможных исходов измерения (см. рис. ниже) не позволяют извлечь энергию.
Более интересные эффекты можно наблюдать в случае двух идентичных бозонов или фермионов при температуре, близкой к абсолютному нулю. Для фермионов действует принцип Паули, запрещающий им одновременно находиться в одном квантовом состоянии, вследствие чего f0 приближается к нулю, и извлечь энергию становится сложно. У бозонов, напротив, f0 в идеале равняется 1/3, а при повышении температуры и у фермионов, и у бозонов f0 приходит к значению 0,25, поскольку частицы становятся различимы. Таким образом, на всём интервале температур бозонная машина Силарда оказывается более «полезной».
Наблюдать действие квантовой машины Силарда на практике ещё никому не удавалось. Возможно, её бозонный вариант будет построен на основе системы охлаждённых и захваченных в ловушку атомов.

Слева: варианты расположения двух идентичных бозонов в камере со стенкой. Справа: то же для двух различимых частиц. Если частицы находятся в разных частях камеры, извлечь энергию не получится. (Иллюстрация S. W. Kim et al.)
Полная версия отчёта опубликована в журнале Physical Review Letters;; текст статьи можно скачать отсюда.
Подготовлено по материалам Американского физического общества. UA
UA EN
EN RU
RU
